ルートインホテルズ女子陸上部 創部 東北復興事業計画を発表 15年(平27)2月 4月 「ルートイングループ・永山勝利基金」設立、長野県と協力し奨学金制度を展開 登米コールセンター開設 16年(平28)2月 ベトナム・ダナンに現地法人を設立 17年(平29)4月上の公式によって微分を続けてゆくやり方もありますが、もうすこし単純に多項式の計算してみます。 =abxcx 2 dx 3 ex 4 と展開されるとしましょう。 両辺を2乗して、 1x= (abxcx 2 dx 3 ex 4 ) 2 =a 2 2abx (2acb 2 )x 2 (2ad2bc)x 3 (2ae2bdc 2 )x 4 各項を比較して a 2 =1 より a=1 2ab=1 より b=1/2 2acb 2 =0 より c=1/8ルートって何? ルート(√)は、「平方根」といいます。 ルートという記号の読み方は、「root」 (根、という意味)からきています。 「平方」は、2乗、という意味ですので、2乗の根、ということです。 つまり、2乗すると根から成長して記号が外れる、という仕組みです。 2乗は同じ数字を掛けることですから、√2×√2=2、ということになります。 また、-√2×

幻影彼岸の展開ルートまとめ ニビル登場後 まめしば日記
ルート 展開 近似
ルート 展開 近似-あるルートに進むための条件はフラグと呼ばれる。 転じて、「こんな展開が見たい」「どうしてこうならなかった」というもしもの想像をゲームのルートに例えることもある。 関連タグ フローチャート フラグ マルチエンディング ルート漫画ルート サブアセンブリの PropertyManager にアクセスするには、 ツール(Tools) > ルーティング(Routing) > 電気(Electrical) > 展開ルート(Flatten Route) をクリックします。




ルート計算 展開公式をつかう3つの平方根問題の解き方 Qikeru 学びを楽しくわかりやすく
Selezione delle preferenze relative ai cookie Utilizziamo cookie e altre tecnologie simili per migliorare la tua esperienza di acquisto, per fornire i nostri servizi, per capire come i nostri clienti li utilizzano in modo da poterli migliorare e per visualizzare annunci pubblicitari やり方は式の展開で学んだ方法と同じ →展開の基礎 もちろん初めに、 ①すべて の形に直す ②分母のルートは有理化する というのは変わらない。 (1) すべて の形に直すと ( )の中の項すべてに を掛ければよい。 ・・答 (2)式の展開の電卓 入力された数式を展開する電卓です。少数や分数を含んだ数式の展開にも対応しています。 約分の電卓 分母と分子を入力すると約分された分数を表示する電卓です。大きい数の分数でも簡単に約分をおこなうことができます。 通分の電卓
上の画像の赤枠の必要札は五十音順に並べてあるので、 例えば、ddスワラル・スライムと ddラミアとdd魔導賢者ケプラー を使った展開ルートを探したい場合は 青枠の検索ボックスに ケプラー、スワラル、ラミア と入力することで検索できます。 カード名を省略しているので、以下を参照して展開公式を利用したルートの計算練習問題とポイント解説です。 ルート(√)計算は文字式と同じあつかいができますので展開公式が利用できます。 ルートのついた無理数の性質と展開公式を組み合わせた後は確実に計算するだけです。 「式の計算」が教科書で後になっている人には逆になりますがむずかしくはないので解説を見ながら進めて下さい。プロジェクト構造の設定 PyCharm では、 コンテンツ は現在作業しているファイルのコレクションであり、サブフォルダーの階層に編成されている可能性があります。 プロジェクトの最上位フォルダーは、その コンテンツルート です。 コンテンツルート内では、PyCharm はソースコードを含む
ルートラボロスの展開 年4月5日 / 最終更新日時 年5月9日 あじこぼ 自転車いじり われわれは3月末で長く愛したYahooルートラボを失った目次 000 展開パターン(ZS-昇華賢者アストラル・ホープ) 039 展開パターン(オノマト連携アストラル・ホープ) 124 展開パターン(オノマト連携 ⚫√2×√68+√48 これはまずは一番左のルート同士の掛け算をやってみて。 あとは、√48のルートを簡単にするんだ。 最後に、ルートの中身が同じだったらルートの足し算をしてみよう。 ⚫(2x7)二乗3(x+1)(x1) これは乗法の公式を使って展開するね。




ルート計算 展開公式をつかう3つの平方根問題の解き方 Qikeru 学びを楽しくわかりやすく




中学3年生 数学 平方根のいろいろな計算 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
この「NaN」は「Not a Number」の略で「0で割り算したから数字じゃないものになっちゃいましたよ! 」という意味。 では √x のような関数はどうやって近似するかというと、 x = 0 以外、たとえば x = 1 の回りにテイラー展開する。 x = 1 でなら、 1 2√x x = 1 = 1 2 となってちゃんと値がある。 二階微分も計算しておくと、 d2 dx2√x = − 1 4x3 2 となるから2次の項の係数は 1 2関数の近似とTaylor 展開 微分係数と接線の方程式 実数x の関数f(x) のx0 における微分係数f′(x 0) の定義は次の様に書き換えることが出来る。 lim x→x0 f(x)−f(x0) x−x0 −f′(x 0) = 0 つまり とおくと このことは を の近くで一次関数 で近似すると、 が に近付くとき「余り」 は のルートによる展開の違い レコ ・ アリス はどちらが生存していても展開に大きな違いはないが、アリス生存時の方がアリスの殺人事件について詳しい事実が分かる。 カンナ ・ ソウ はどちらが生存しているかで展開が大きく変わる。 ⇒詳しい変化はこちら ↑



2次無理数の連分数展開 Takapの数学日記



1
ルートとは?平方根の求め方を解説!分数や小数の場合はどうやる?←今回の記事 平方根、ルートの値を語呂合わせ!覚え方まとめ a√bの形に変形するやり方とは? 平方根の大小関係を不等号で表す問題を解説! 根号を含む式の値の求め方とは? i のルートを求める方法1 ( a b i ) 2 = i ( a , b (abi)^2=i\(a,b ( a bi ) 2 = i ( a , b は実数)を解けばよい。 展開する: a 2 − b 2 2 a b i = i a^2b^22abi=i a 2 − b 2 2 abi = i 中学レベル平方根(ルート√)の展開について 平方根(ルート√)の展開方法を教えてください。 以下のような平方根がある場合、どのように展開をすれば良いでしょうか。 またどのような場合、ルート√から展開出来ないと判断できるのでしょうか。




ルートの分数計算 問題解説で完全マスターだ 数スタ




中3数学 平方根2 5 加減 展開 復刻版 Youtube
はじめに こんにちは。ぐちゃです。 以前、《空牙団の大義 フォルゴ》を手札1枚から出すという記事を投稿したのですが、記事を作成しているときに得た知見で《ライトロード・ドミニオン・キュリオス》も手札1枚から出せるギミックをいくつか見つけたのでこちらも記事にすることにしこの PropertyManager にアクセスするには、ルート サブアセンブリを展開し、 ツール(Tools) > ルーティング(Routing) > 電気(Electrical) > 展開ルート(Flatten Route) をクリックします。 信頼された証明書プロファイルを作成して展開すると、Intune のマネージド デバイスに信頼されたルート証明書が展開されます。 信頼された証明書プロファイルにより、Microsoft Intune での Simple Certificate Enrollment Protocol (SCEP) および Public Key Cryptography Standards (PKCS) 証明書プロファイルの使用が




数学 中3 17 ルートの変形 Youtube




数学 A B C 二乗の展開公式は 問題の解き方は徹底解説 数スタ
ルートの展開は以前紹介した展開公式を使います。 ・ルートの展開をしよう。 ②の問題は(x+2)(x+5)=x 2 ③の問題は(x+4)(x-4)=x 2 -4 2 ④の問題は、(x+1) 2 =x 2 2 ⑤の問題は、(x-3) 2 =x 2 2 の展開公式を使って解くことができます オイラーの公式 テイラー展開を使うことでオイラーの公式という不思議な式を簡単に導くことができます。 eの肩に虚数が乗っていて、なぜかそれが三角関数に分解できるというのがオイラーの式です。 いっけん成り立たなそうですが、xに円周率を入れると以下のようになります。 今度はなぜか1になりました。 実際にテイラー展開を使って計算して本当 目次 ・前書き ・基本展開ルート イゾルデ1枚からの先攻制圧 ・派生ルート解説 ・3ハンデス「ネオスペース・コネクター」+オリヴィエ ・ニビルケアオリヴィエ+オジエ+自己SS可能な戦士




中学3年生 数学 平方根のいろいろな計算 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




トヨタのmaasアプリ My Route 全国展開へ 春に横浜など順次拡大 Impress Watch
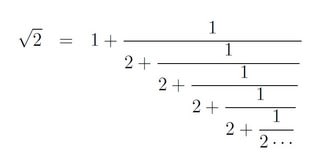
動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru ルート2の連分数展開と長方形 上で見た通り、 $\sqrt{2}$ の連分数展開は次のようになります。 \begin{eqnarray} \sqrt{2}=1\frac{1}{ \displaystyle 2\frac{1}{ \displaystyle 2\frac{1}{ 2\ddots }}} \end{eqnarray}これと図形とをリンクさせて考えてみましょう。正の数 a に対して, a の平方根のうちで負の数の方を で表し,マイナス・ルート a といいます.これは, の符号だけを変えたものです. 例7 の2つですが,そのうちの負の方を で表します. だから, です. 例8




ルートと式の展開が混ざった式が苦手で どなたか教えてくださいっ Clear
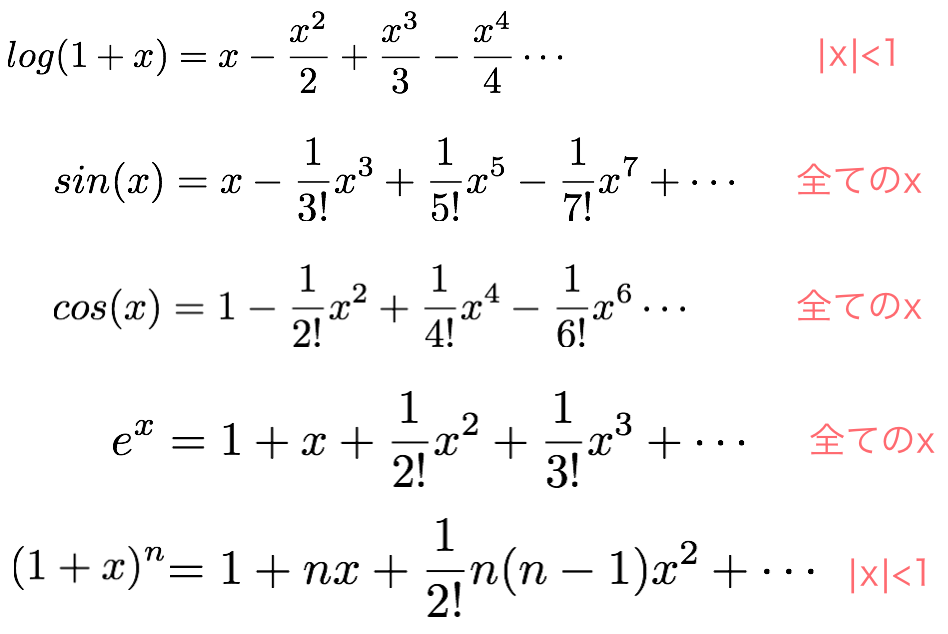



マクローリン展開 例題 ルート



ルート計算 展開公式をつかう3つの平方根問題の解き方 Qikeru 学びを楽しくわかりやすく




Find 鉄獣戦線の展開ルートを考えていたのですが レスキューフェレットから先が選択肢多すぎてパンクしたので一旦置いておきます 強いやり方があれば教えてください




このようにどうしてなるのか分からないので 途中式を教えていただけますか ルート3の Clear




ルート計算 展開公式をつかう3つの平方根問題の解き方 Qikeru 学びを楽しくわかりやすく



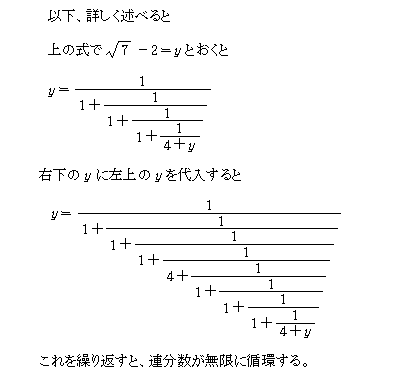
ルート7の連分数展開 Takapの数学日記
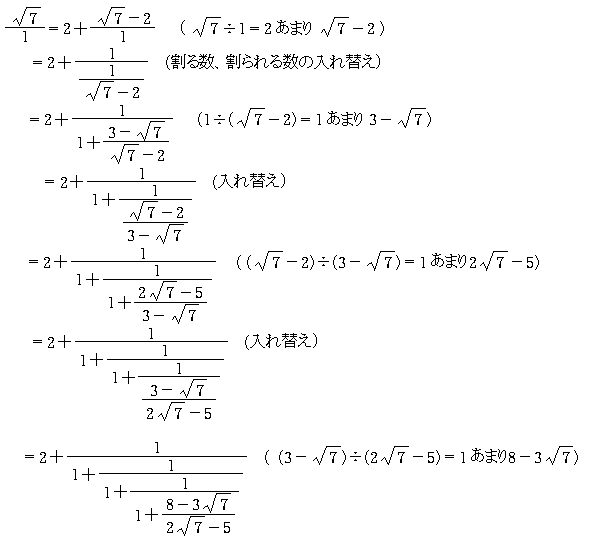



ルート7の連分数展開 Takapの数学日記




ルート計算 展開公式をつかう3つの平方根問題の解き方 Qikeru 学びを楽しくわかりやすく




ルート Inventor Autodesk Knowledge Network



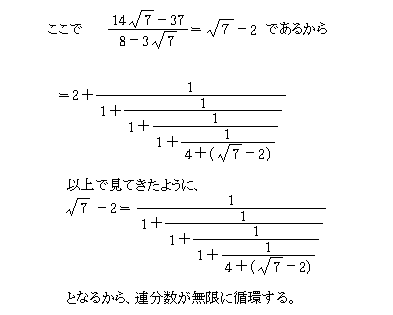
7を連分数展開 6は 本の例題 3 どおりにやってできたのですが 写 Yahoo 知恵袋




コレクション ルート 展開 近似 ルート 展開 近似
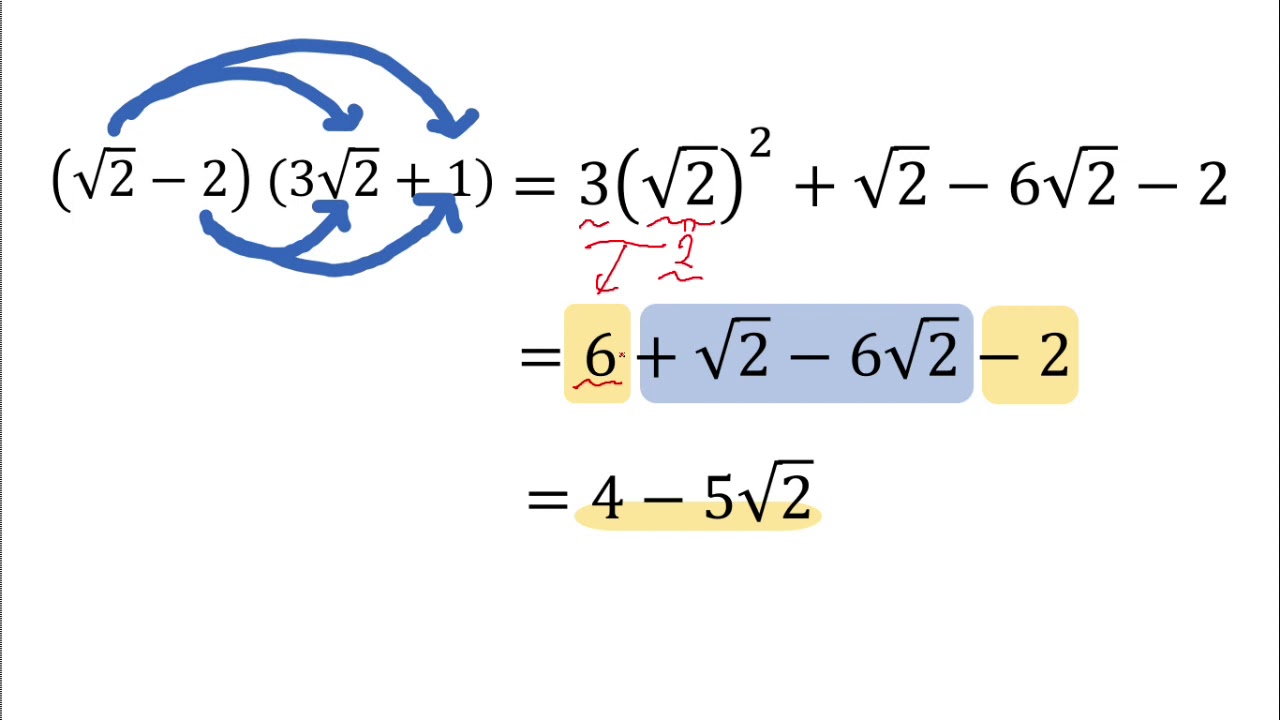



中3数学 ルートを含む式の展開のやり方を解説 Youtube



画像 ルート 展開 公式 ハイキュー ネタバレ




六花の展開ルート紹介 構築の逆転




高校 数学 数と式33 根号と展開公式 12分 Youtube



ルートサンプリング 株式会社エフ エージェンシー




中学数学 平方根 のコツ 有理化 加減乗除 展開




ルート計算 展開公式をつかう3つの平方根問題の解き方 Qikeru 学びを楽しくわかりやすく




中学数学 平方根 のコツ 有理化 加減乗除 展開




展開の利用 ドリるーむ




展開ルート



非接合ルートの展開 19 Solidworks ヘルプ



1
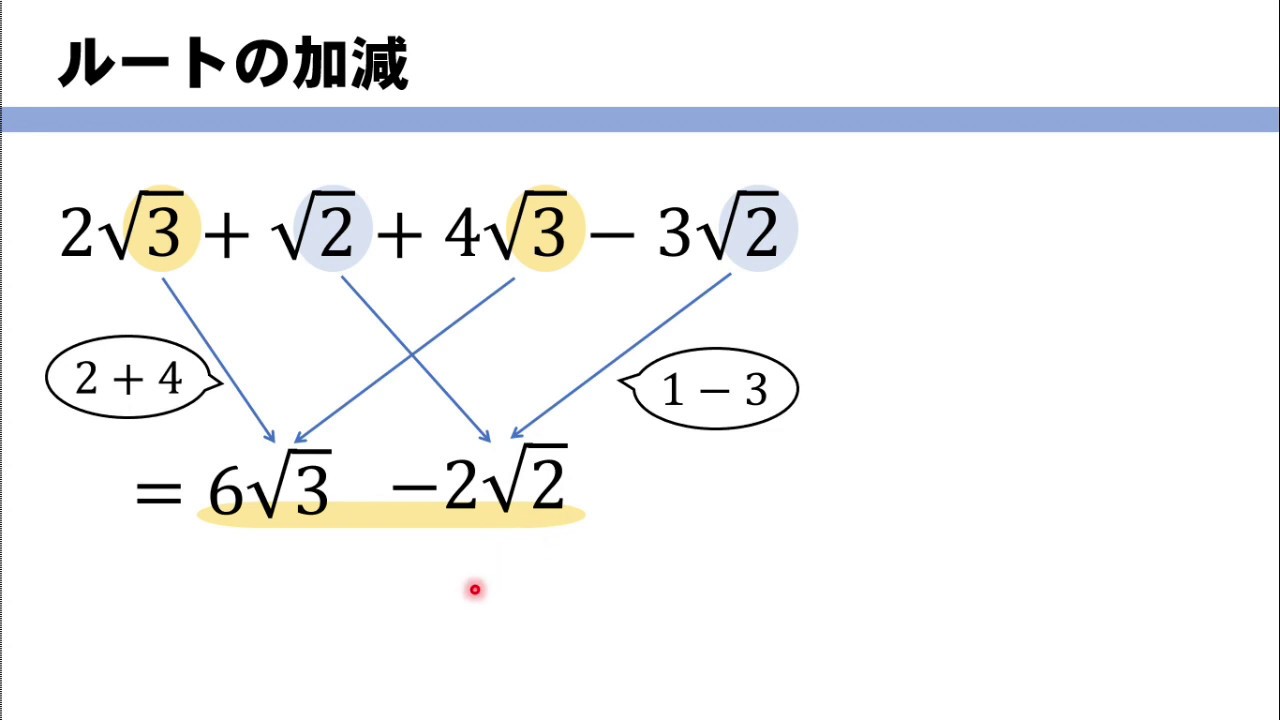



平方根 ルートの計算方法まとめ 問題を使って徹底解説 数スタ




商品詳細 平方根 ルート展開 Tシャツ グリーン デザインtシャツ通販clubt



3




展開ルート



数学 Xのテイラー展開 無限級数 Twilightのまったり資料室 ブログ




展開する式なんですけど 約分すると プラマイとルート6が残るんですけど 答える時は Clear




ルート計算 展開公式をつかう3つの平方根問題の解き方 Qikeru 学びを楽しくわかりやすく
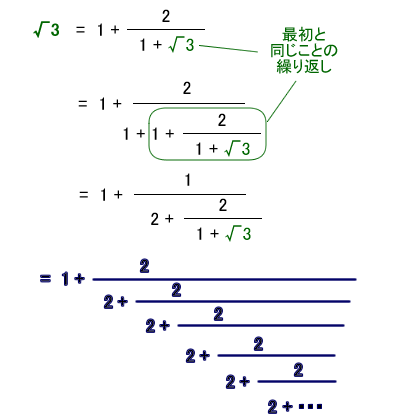



いまひとつの連分数展開 小人さんの妄想




数学 中3 23 ルートの問題をつめこんでみた Youtube



ルートの展開 Flattening The Route 10 Solidworks ヘルプ
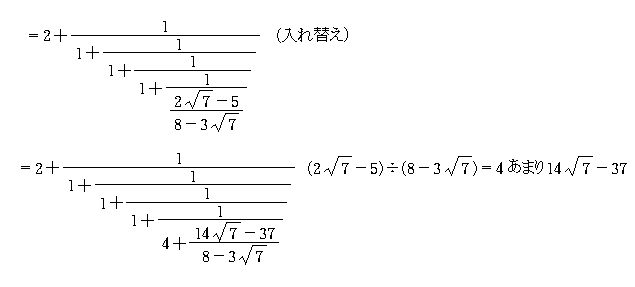



ルート7の連分数展開 Takapの数学日記




商品詳細 平方根 ルート展開 Tシャツ グレー デザインtシャツ通販clubt




羽田新ルート 急展開に 住民不在 爆音 落下物 不安尽きず 東京新聞 Tokyo Web
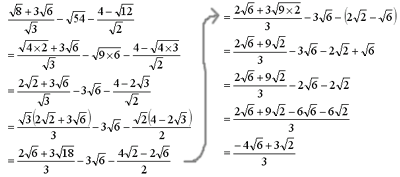



中学の数学 ルートの計算方法って Sakura Scope




ルート計算 展開公式をつかう3つの平方根問題の解き方 Qikeru 学びを楽しくわかりやすく




2の平方根 Wikipedia
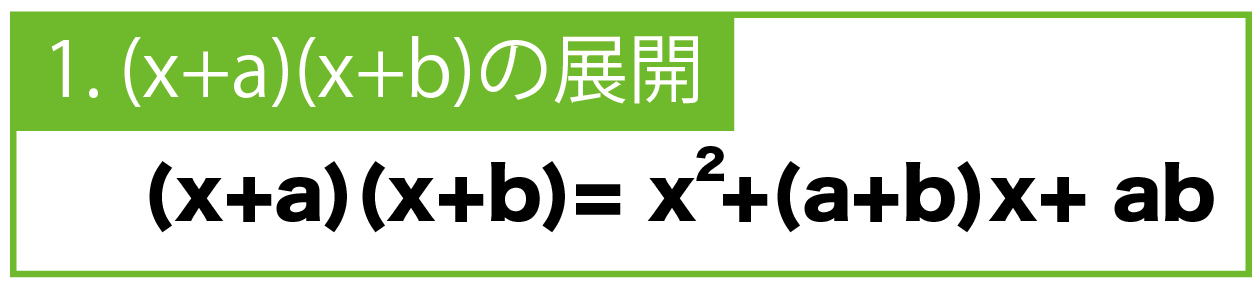



ルート計算 展開公式をつかう3つの平方根問題の解き方 Qikeru 学びを楽しくわかりやすく




数学 中3 15 平方根 Youtube




中3数学 ルートを含む式の展開のやり方を解説 Youtube




商品詳細 平方根 ルート展開 Tシャツ グレー デザインtシャツ通販clubt




ルートの中にルート 二重根号のはずし方について解説 数スタ



ルートサンプリング 株式会社エフ エージェンシー




ルート5の連分数展開で写真の式をもう少しわかりやすくして欲しいです Clear




平方根の足し算と引き算 ルート計算のやり方や分数の求め方 リョースケ大学




ひぐらし業の新ルート展開に興奮して描きたくなった しゃーのイラスト




ルート2が無理数であることの4通りの証明 高校数学の美しい物語




ルートの展開 展開公式と同じ解き方で計算しよう 中学や高校の数学の計算問題




ルート計算 展開公式をつかう3つの平方根問題の解き方 Qikeru 学びを楽しくわかりやすく




最高のコレクション ルート 展開 計算機 ハイキュー ネタバレ




複雑なルートの分数の有理化のやり方と問題 理系ラボ




平方根 式を展開する 苦手な数学を簡単に



21 Whatsnew 展開されたルート内のテーブルの位置




99 Ou Plus ルート 展開 ルート 展開 近似



展開ルート編集の機能強化 17 Solidworks 新機能



中学の数学 ルートの計算方法って Sakura Scope




裏技公開 11のような平方根を速く求める方法 連分数使います Cupuasu クプアス




幽鬼うさぎを使った展開ルートまとめ Ddd研究所




最高のコレクション ルート 展開 計算機 ハイキュー ネタバレ




中学3年の数学 動画 ルートと展開のコラボの問題 19ch




平方根の足し算と引き算 ルート計算のやり方や分数の求め方 リョースケ大学




平方根 式を展開する 苦手な数学を簡単に




4月制限 3軸シンクロ 展開ルートとデストルドガイザー ソリティアで勝つことを目指して 遊戯王ブログ




ルート3の近似値の求め方4パターン 数学の星




中3数学 ルートの計算とカッコ カッコの公式 練習編 映像授業のtry It トライイット




全ての日本企業の海外展開の成功のために ゴールデンルート を徹底研究 Digima 出島 と 明治大学 奥山雅之研究室 地域産業研究 が共同研究をスタート 株式会社resorzのプレスリリース
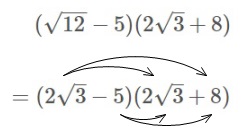



展開公式を利用するルートのついた無理数の計算問題とポイント




ルート計算 展開公式をつかう3つの平方根問題の解き方 Qikeru 学びを楽しくわかりやすく



3




中3数学 2 10 ルートの計算 展開を使うタイプ Youtube




六花の展開ルート紹介 構築の逆転



ルート7の連分数展開 Takapの数学日記
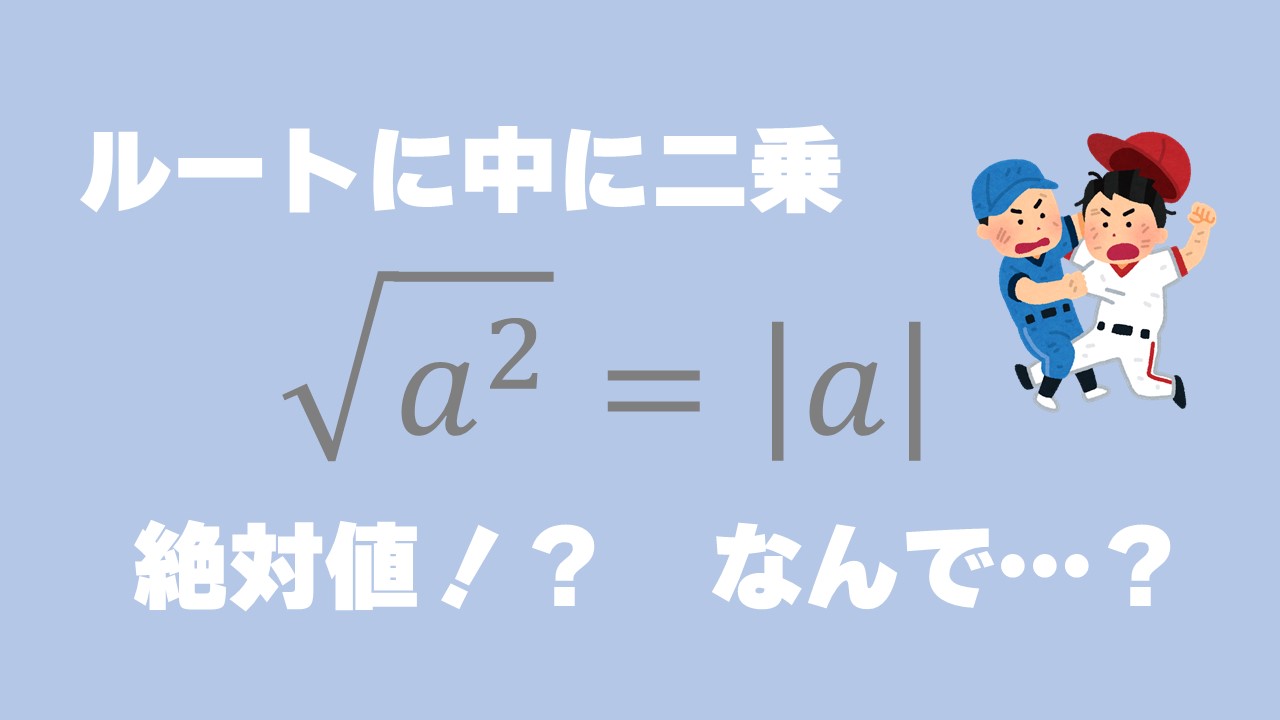



ルートの中身が絶対値に なんで場合分けが必要なのか 数スタ




中学数学 平方根 のコツ 有理化 加減乗除 展開




トヨタと西鉄 マルチモーダルモビリティサービス マイルート を福岡 北九州で本格展開 レスポンス Response Jp




ルートは式の可視化ができるかどうかで理解度がわかる 受験に強くなる子どもとの接し方




幻影彼岸の展開ルートまとめ ニビル登場後 まめしば日記




平方根の問題の解き方 6パターン 数学fun




My Route マイルート トヨタのマルチモーダルモビリティサービス全国展開へ Moby モビー




愛されし者 ルート 計算 足し算




トヨタのmaasアプリが全国展開へ バス 鉄道 カーシェアなどを組み合わせた




中3数学 平方根 3 7 根号を含む式の展開 Youtube



ルート計算 展開 を教えて下さい 写真の計算はどのように Yahoo 知恵袋




中3数学 ルートの計算とカッコ カッコの公式 練習編 映像授業のtry It トライイット




最高のコレクション ルート 展開 計算機 ハイキュー ネタバレ




Twitter पर まべに 真紅眼守護竜展開ルート 黒鋼竜 チューナー出すカード 盤面 天球 相手ターンに真紅眼に変換 アビス サベージ 牙2枚 渓谷 5妨害 手札2枚




数学 中3 22 ルートと展開のコラボ Youtube




ルート計算 展開公式をつかう3つの平方根問題の解き方 Qikeru 学びを楽しくわかりやすく




平方根 式を展開する 苦手な数学を簡単に




ルート2を連分数の極限として求めようとしたら行列が出てきた 前編 しいたげられたしいたけ




ルート テスト スイートの全テスト ケースを展開 折りたたむ Synapsert



0 件のコメント:
コメントを投稿