Ⅰ 歴史 三平方の定理は別名「 ピタゴラスの定理 」と呼ばれています。 しかし、実際にこの定理を発見したのはピタゴラス(Pythagoras, BC569頃BC500頃)ではなく、彼が生まれる約1000年前からバビロニアで知られていました。 ピタゴラスは若い頃に、エジプトやバビロニアを旅し
ピタゴラスの定理 計算- 光速の60パーセントの速度で航行する宇宙船内の時間の遅れの計算 ここで、せっかくなので、実際に、 上記のピタゴラスの定理を用いた数式を使って、実際に 特殊相対性理論において生じる時間の遅れを計算 してみることにします。 すると、例えば、 平面 (普通の数学)だと、a*a b*b = c*c になると思います。 ↓ #include float c = sqrt (a*a b*b);
ピタゴラスの定理 計算のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  | 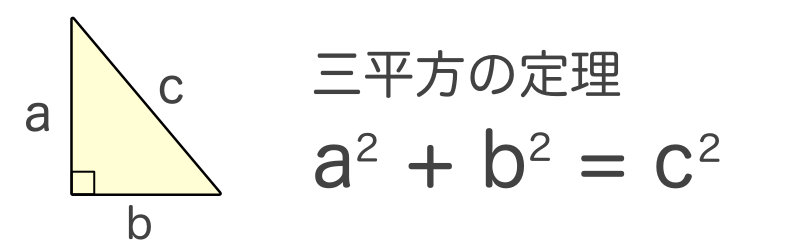 |
 |  | |
「ピタゴラスの定理 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  |  |
「ピタゴラスの定理 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  | |
 |  |  |
「ピタゴラスの定理 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
 |  |  |
「ピタゴラスの定理 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
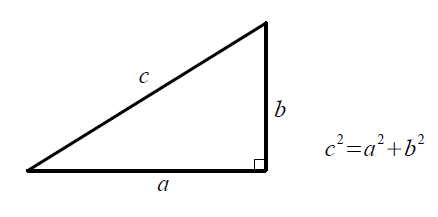 |  |  |
「ピタゴラスの定理 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  |  |
「ピタゴラスの定理 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
 |  | |
「ピタゴラスの定理 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  | |
「ピタゴラスの定理 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | 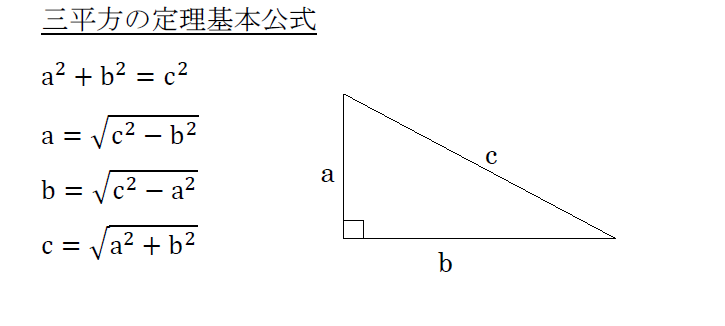 |
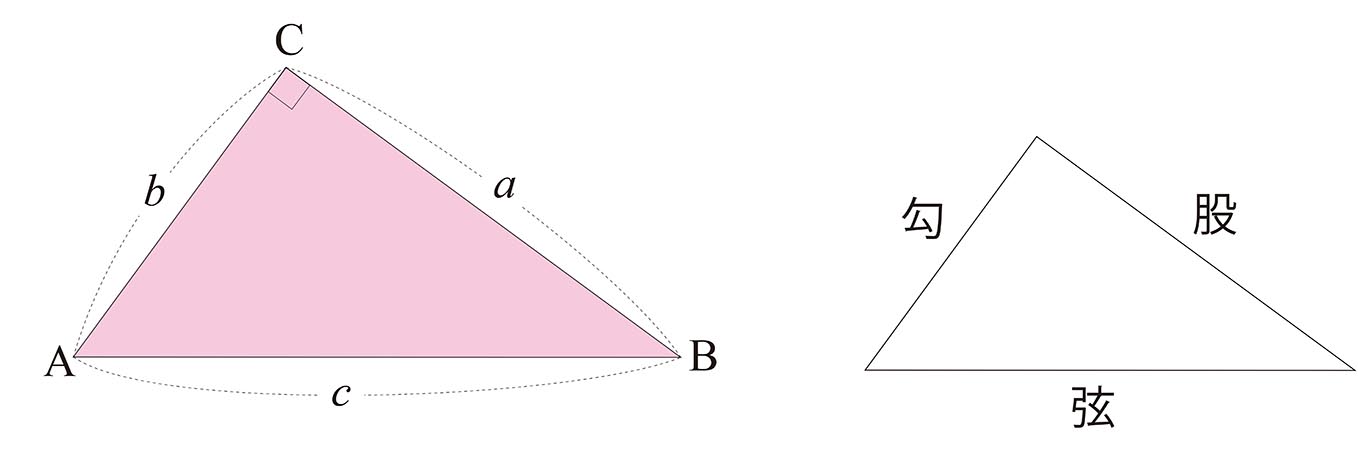
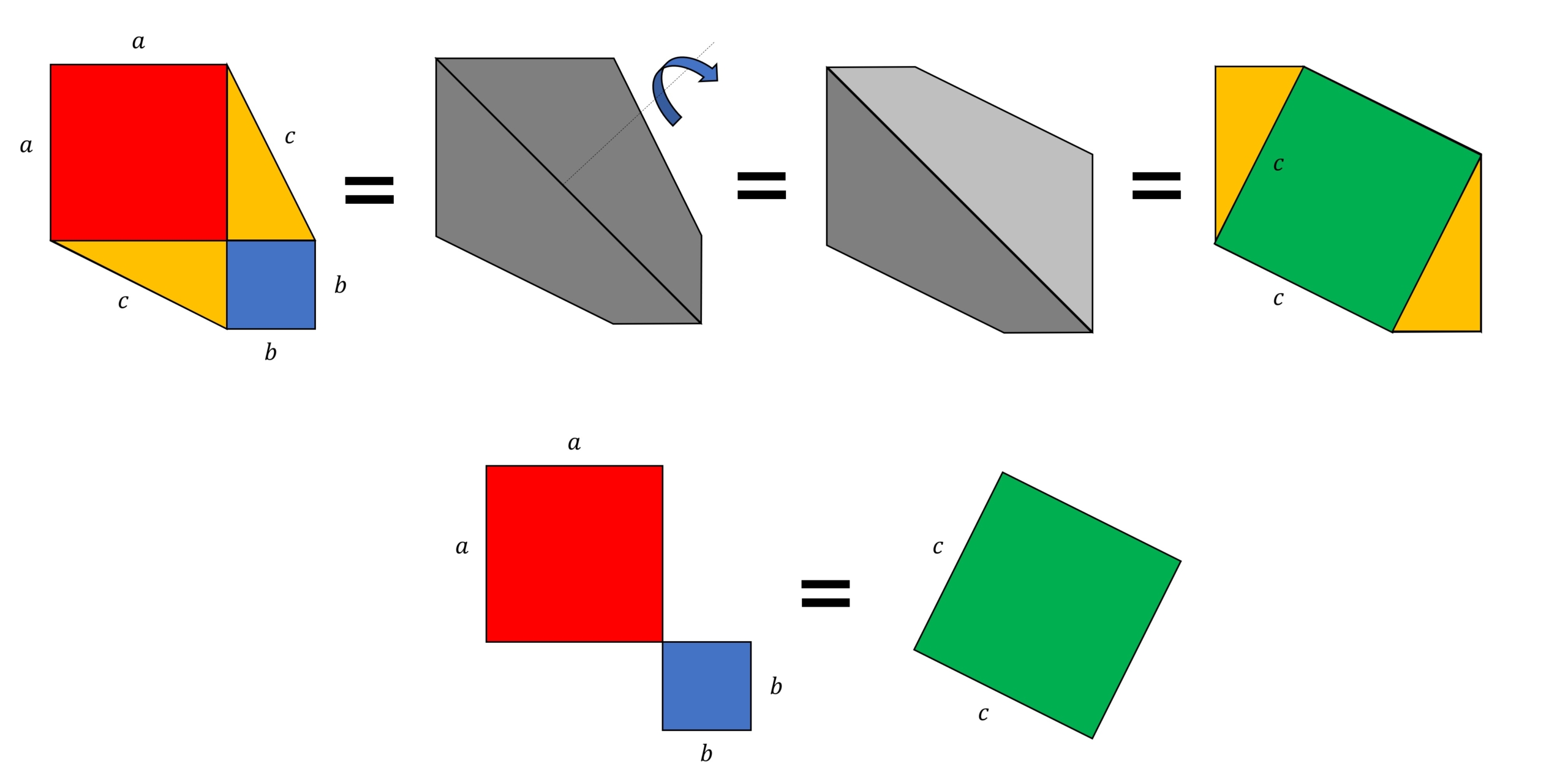
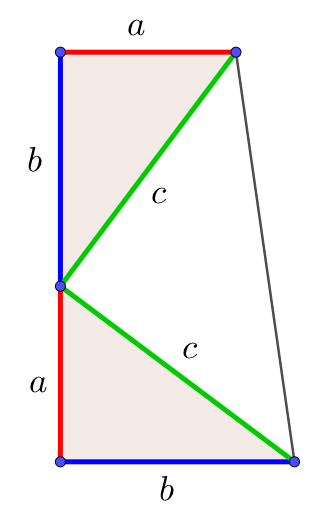
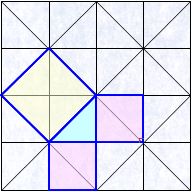
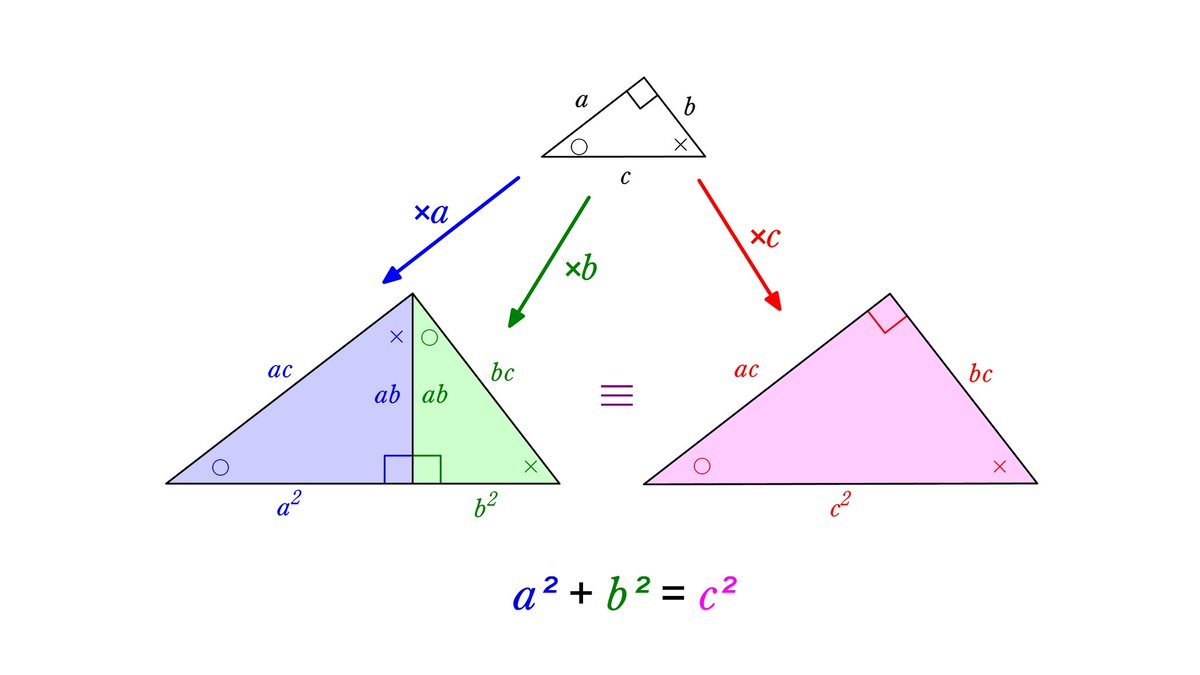
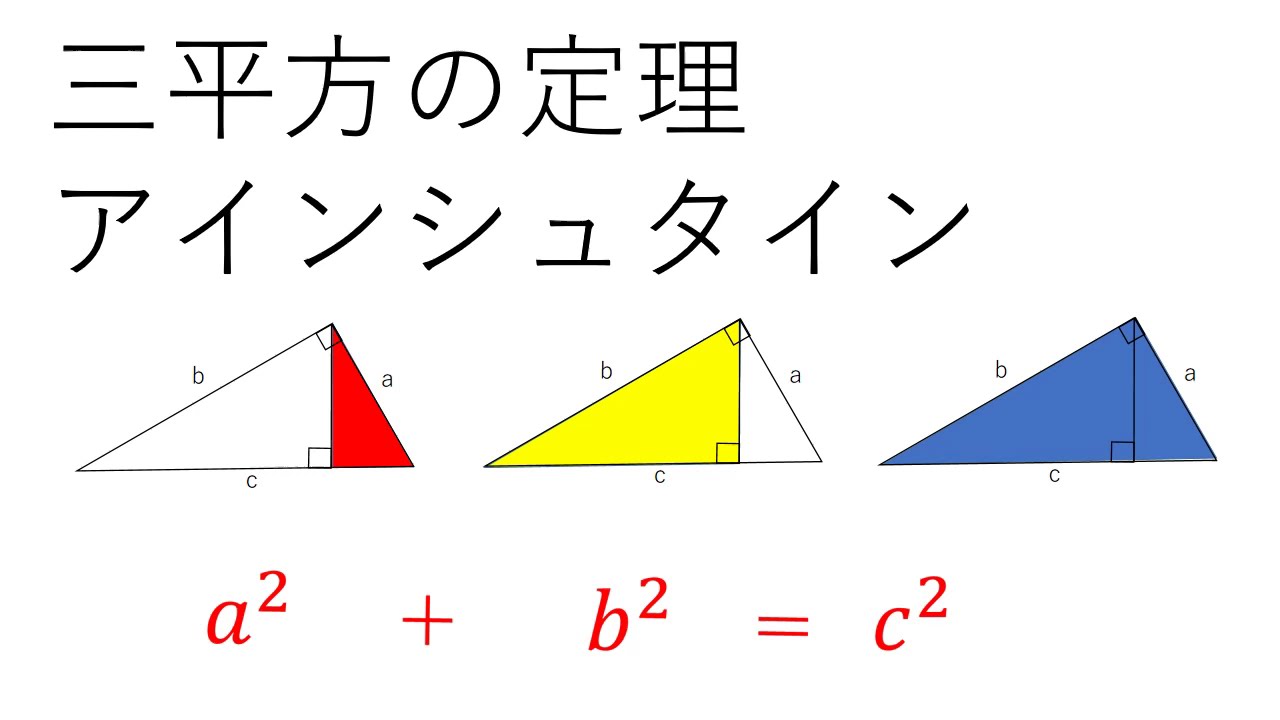
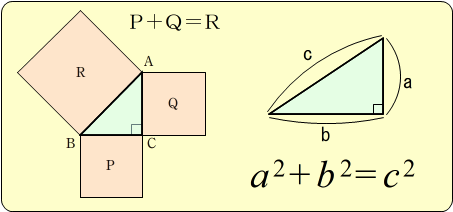
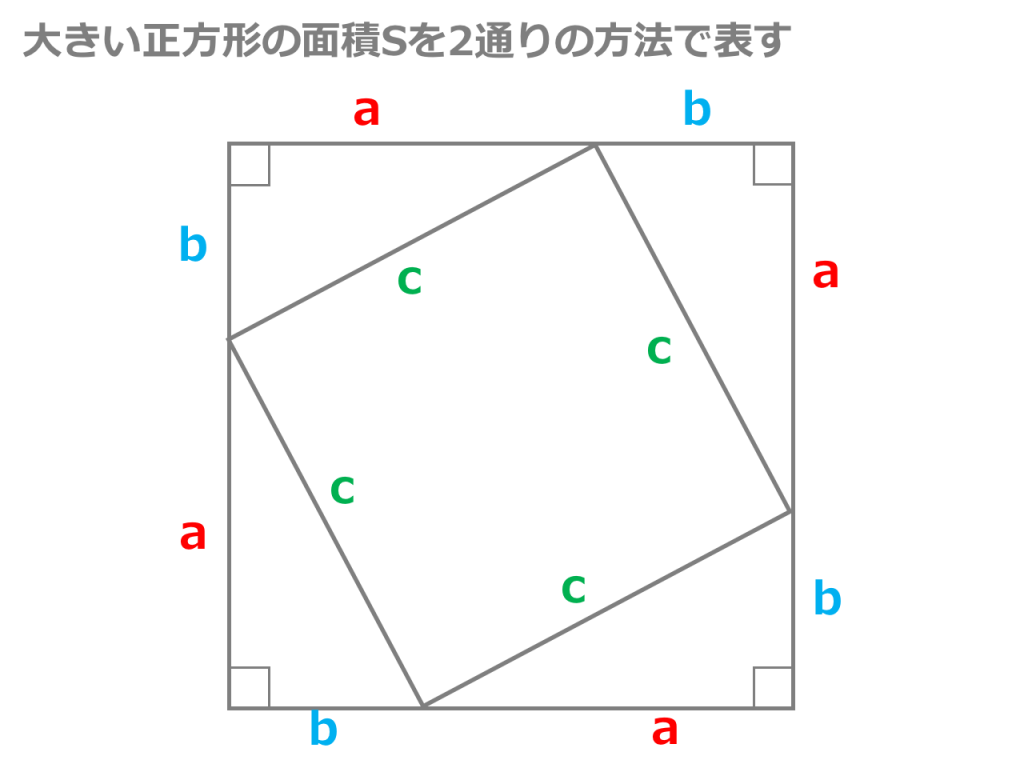
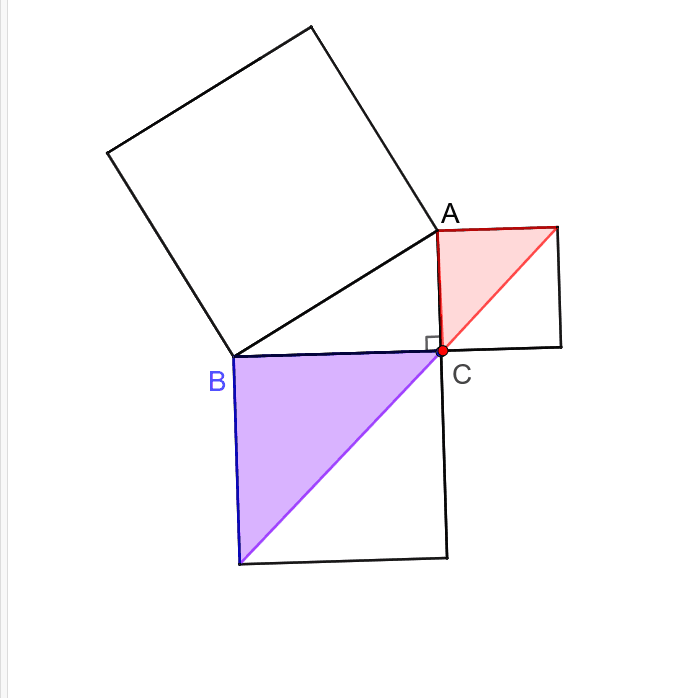
三平方の定理は、別名「ピタゴラスの定理」とも言います。 例えば、直角をはさむ2つの辺の長さが \(3cm\) と \(4cm\) の直角三角形の斜辺の長さを実際に測ってみると、\(5cm\) であることが分かりま☆ 動機 三平方の定理を満たす3つの自然数(ピタゴラス数)、3,4,5、5,12,13は知っているが、 ほかにピタゴラス数はあるのか、あるなら100個以上見つけたいと考えたから ☆ピタゴラス数の定義
Incoming Term: ピタゴラスの定理 計算, ピタゴラスの定理 計算サイト, ピタゴラスの定理 計算問題, ピタゴラスの定理 計算方法, ピタゴラスの定理 計算式, ピタゴラスの定理 計算機, ピタゴラスの定理 計算 半径, ピタゴラスの定理 計算90度求める,




0 件のコメント:
コメントを投稿